傅里叶变换

本文是 如果看了此文你还不懂傅里叶变换，那就过来掐死我吧 的精华版。目的就是要让你在不看任何数学公式的情况下理解傅里叶分析。如果有兴趣且有耐心的话可以点击阅览原文。

首先 cite 一下原作者：

作 者：韩 昊
知 乎：Heinrich
微 博：@花生油工人
知乎专栏：与时间无关的故事
谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。
转载的同学请保留上面这句话，谢谢。如果还能保留文章来源就更感激不尽了。

任何一种波形，都可以看作若干幅度、相位、频率不同的正弦波的叠加。我们首先用方波举个例子：

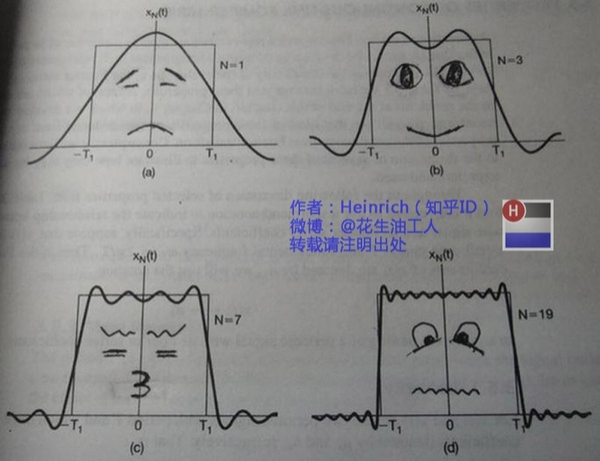
如果我们把叠加方波所需的若干个正弦波展开，会得到如下所示的图像。

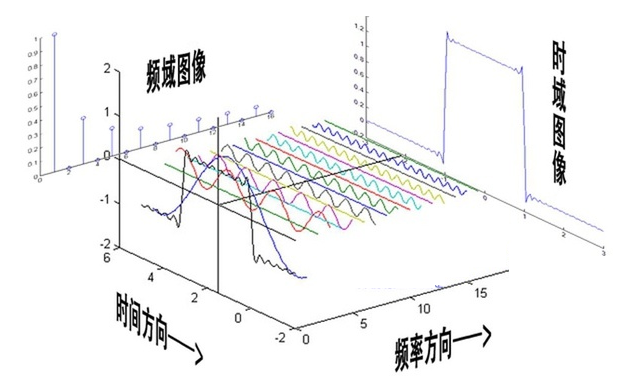
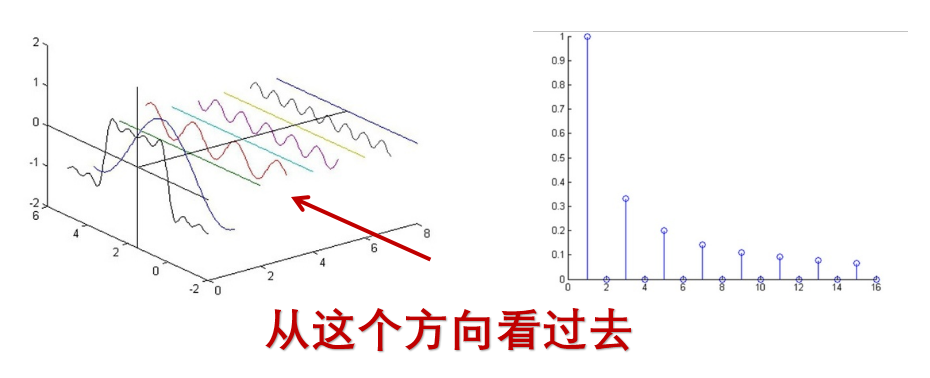
我们从时间方向去观察这个波形，就会得到信号的时域图像（也就是方波）。如果我们从频率方向去观察这个信号，就会得到信号的频域图像。

不过，上图的表示其实并不全面。每个频率的信号对应的信息不仅有强度，而且还有相位。从下图来看，如果箭头所指向的信号的相位发生了变化（即向左或向右移动），那么叠加合成的波形也将发生变化。

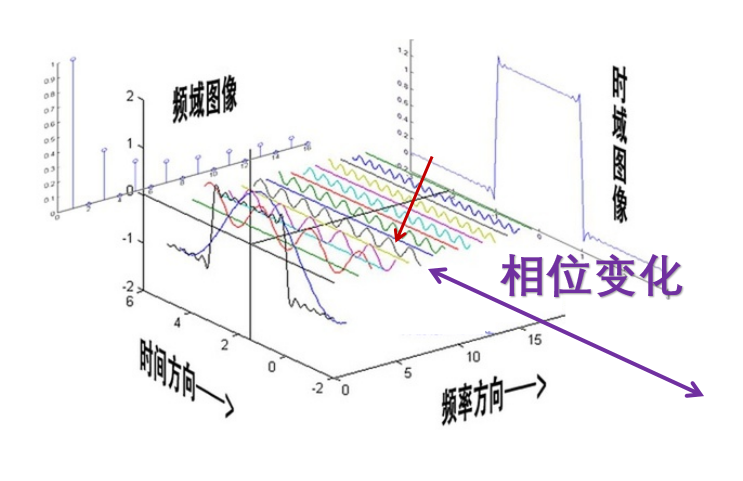
所以，傅里叶变换的结果是一个复数的数组，其中每一个复数代表某一频率上信号的强度和相位的信息。

复数的模长表示强度，复数的角度表示相位。

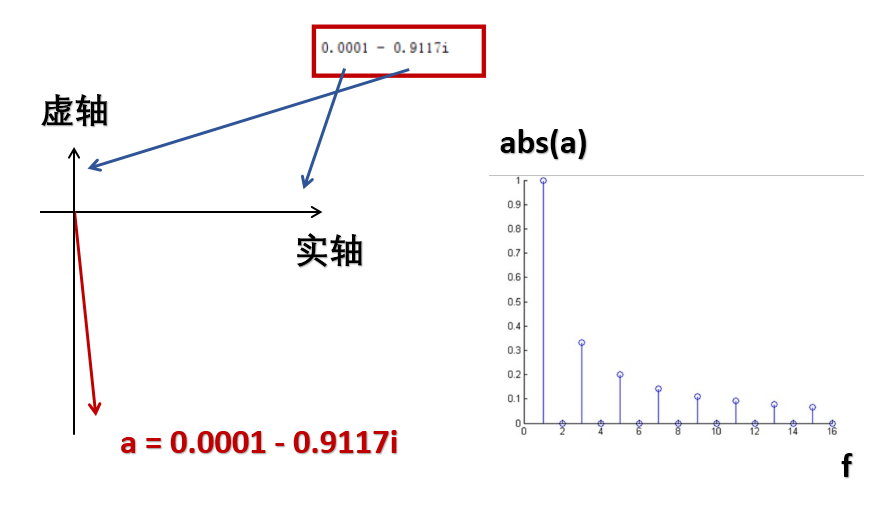
信号的时域表示和频域表示是等价的，得到其中一个就可以得到另一个。如果有时域信号，可以使用傅里叶变换得到频域信号。如果有频域信号，则可以使用逆傅里叶变换得到时域信号。